Sponsored Post
Vehicles that drive themselves present a new and demanding set of computational problems. First, there’s perception: the immediate acquisition of sensory data surrounding the vehicle from cameras, RADAR, LIDAR, and position detection devices. Then, analysis, prediction, and planning to determine the instantaneous path and speed the vehicle should take. Finally, there’s actuation: controlling the vehicle’s steering, speed, and brakes. All this must run in real time with extremely strict end-to-end latency requirements.
Central to this unique process is Kalman filtering, a statistical algorithm that was developed in the 1960s and has been found useful for robotic motion planning and control, as well as signal processing and econometrics. In particular, the Extended Kalman Filter algorithm (EKF) is used to make predictions about the state of the vehicle (position, direction, speed, etc.). The EKF has two consecutive steps over several iterations:
- The prediction step estimates values of current variables and their uncertainties based on motion models, including changes in values over time.
- The update step updates the predicted estimates based on a weighted average of the predicted estimate and the estimate from the current measurement, with higher weights implying lower uncertainty.
For example, EKF predicts the position of the vehicle and its velocity from noisy LIDAR and RADAR sensor measurements. By fusing both RADAR and LIDAR data, a coupled estimate of the vehicle’s position acquires a higher accuracy than by using noisy LIDAR and RADAR by themselves.[clickToTweet tweet=”Intel MKL speeds Karman Filtering for automated driving apps.” quote=”Intel MKL speeds Karman Filtering for automated driving apps.”]
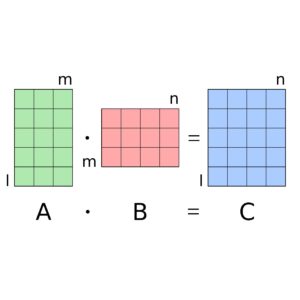
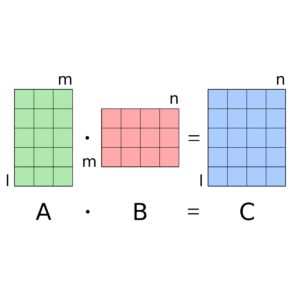
The automated driving developer community typically uses Eigen*, a C++ math library, for the matrix operations required by the EKF algorithm. Turns out that EKF usually involves many small matrices (specifically, when the sum of dimension sizes is less than 20). However most HPC library routines for matrix operations are optimized for (very) large matrices.
The Intel Math Kernel Library (Intel MKL) provides highly optimized, threaded, and vectorized math functions that maximize performance on Intel Xeon® processors. Intel MKL provides highly-tuned xGEMM function for matrix-matrix multiplication, with special paths for small matrices. Eigen can take advantage of Intel MKL through use of a compiler flag.
A significant speedup results when using Eigen and Intel MKL and compiling the automated driving apps with the latest Intel C++ compiler.
Download Intel® Math Kernel Library for free.