A team of researchers at ETH Zurich are working on a novel approach to solving increasingly large graph problems. Large graphs are a basis of many problems in social sciences (e.g., studying human interactions of different types), bioinformatics, computational chemistry, medicine, cybersecurity, healthcare, and many others. However, as graphs grow to trillions of edges, they require unprecedented amounts of compute power, storage, and energy.
Lowering the size of such graphs is increasingly important for academia and industry: It would offer speedups by reducing the number of expensive disk operations, the amount of data communicated over the network, and by storing a larger fraction of data in caches. To enable this, a group of researchers from ETH Zurich, led by Maciej Besta and Torsten Hoefler, argue that the next step towards significantly higher performance and storage reductions in graph analytics can be enabled by lossy graph compression and the resulting approximate graph processing.
As the size of graph datasets grows larger, a question arises: Does one need to store and process the exact input graph datasets to ensure precise outcomes of important graph algorithms? After an extensive investigation into this question, the ETH researchers have been nominated for the Best Paper and Best Student Paper Awards at SC19.
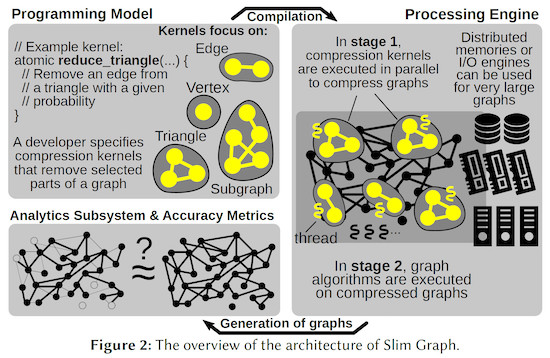
The first core outcome of their research work is Slim Graph: the first programming model, processing framework, compression method, and analysis system for practical lossy graph compression that facilitates high-performance approximate graph processing, storage, and analytics. Slim Graph enables the developer to easily develop numerous graph compression schemes using small and programmable code snippets called compression kernels. Such kernels are executed in parallel by the underlying Slim Graph engine, isolating developers from complexities of parallel and distributed programming. The ETH researchers use their kernel paradigm to implement novel graph compression schemes that preserve numerous graph properties, for example connected components, minimum spanning trees, cuts, or graph spectra. Finally, they incorporate concepts from mathematical statistics to enable a systematic approach for assessing the accuracy of lossy graph compression algorithms.
Are We in Urgent Need of the JPEG Equivalent for Irregular Data?
Until now, one could resort to traditional methods for lossless graph compression,” says Besta. “Unfortunately, it usually incurs expensive decompression in performance-critical code portions and high preprocessing costs. Moreover, as shown recently, the associated storage reductions are not large, because today’s graph lossless compression methods approach theoretical storage lower bounds: fundamental limits on how one can reduce the size of data.”
This analogy between compressing graphs and bitmaps brings immediate numerous questions. First, what is the criterion (or criteria?) of the accuracy of lossy graph compression? It is no longer a simple visual similarity as with bitmaps. Next, what is the actual method of lossy compression that combines large storage reductions, high accuracy, and speedups in graph algorithms running over compressed datasets? Finally, how to easily implement compression schemes?

In Figure 1, we show that, in analogy with the JPEG compression, one may not always need the full precision while processing graphs.” says Hoefler.
The First Model and Framework for Lossy Graph Compression… And It Goes Distributed
To answer these and related questions, we develop Slim Graph: the first programming model and framework for lossy graph compression,” explains Hoefler. “Here, a developer constructs a simple program called a compression kernel. A compression kernel is similar to a vertex program in systems such as the well-known Google’s Pregel processing system. However, the scope of a single kernel is more general than a single vertex — it can be an edge, a triangle, or even an arbitrary subgraph. Second, the goal of a compression kernel is to remove certain (specified by the developer) elements of a graph. In this work, we introduce kernels that preserve graph properties as different as Shortest Paths or Chromatic Number. To ensure the generality of our compression model, we analyzed more than 500 papers on the theory of graph compression, ensuring that Slim Graph enables expressing and implementing all major classes of lossy graph compression.”
The Slim Graph system even enabled the ETH researchers to conduct the first distributed-memory graph compression, reducing the size of the largest publicly available graph dataset, called Web Data Commons. For this purpose, they used Piz Daint, the largest supercomputer operated by the CSCS Supercomputing Centre in Switzerland, having the 6th location on the June 2019 Top500 list.
A Novel Versatile Lossy Graph Compression Algorithm
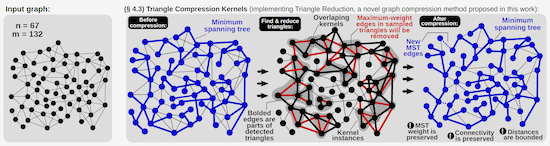
Besides proposing a general system and approach for implementing lossy graph compression, the authors also use Slim Graph to design a new compression algorithm that is versatile – it preserves numerous relevant properties of graphs that are perceived as important by the practice of graph analytics.
Our algorithm, called Triangle Reduction, is versatile: removing certain parts of graph triangles does not significantly impact a surprisingly large number of graph properties, such as the number of connected components, the weight of the minimum spanning tree, distances between vertices, and even cuts,” describes Lukas Gianinazzi, a member of the ETH team and a co-author of the paper.
Kernel-Centric Graph Compression
The scientists discovered the Triangle Reduction compression method by applying the principles of kernel-centric graph analytics, a general paradigm which is being developed by Besta and Hoefler. “This type of programming abstraction allows us to quickly prototype different compression methods without having to implement them from scratch.” says Besta.
Going Interdisciplinary with the Kullback-Leibler Divergence
However, the abstraction, the framework with its evaluation, and the compression algorithm are not everything. The ETH group also investigated the methods for analyzing whether and to what extent different lossy compression algorithms impact the accuracy of a wide number of graph properties and algorithms. “In the process, we first used the fact that some important graph properties and results of algorithms can be modeled with certain probability distributions. For example, in PageRank, one assigns each vertex (that models a web page) the probability (rank) of a random surfer landing on that page. In such cases, we observed that one can use the concept of a divergence — a tool from mathematical statistics that measures the distance between probability distributions — to tell the difference between the original and the compressed graph. For several reasons explained in the paper, we selected the so called Kullback-Leibler divergence which – thanks to its theoretical roots in statistics and information theory – assesses the loss of information in graphs compressed by Slim Graph. ” explains Besta.
Bridging Theory and Practice for Fundamental Insights and High Performance
To support the evaluation of Slim Graph, the group conducted a theoretical analysis, presenting or deriving more than 50 bounds that illustrate how graph properties change under different compression methods provided in Slim Graph. As the group expressed, “We hope that Slim Graph with its approach and methods may become the common ground for developing, executing, and analyzing emerging lossy graph compression schemes.”.
Combining the Best of the Past with the New of Today for Extreme-Scale Irregular Data Analytics
The described lossy graph compression research is an important element of a systematic effort towards accelerating largest-scale irregular data analytics, pursued by Maciej Besta and Torsten Hoefler for a number of years, with a goal of reaching new frontiers of performance and comprehension of this fascinating domain. The newest SC19 outcome draws from related past results in scalable distributed computing that already earned Maciej and Torsten best paper awards at several HPC conferences in the previous years.
References:
Maciej Besta, Simon Weber, Lukas Gianinazzi, Robert Gerstenberger, Andrey Ivanov, Yishai Oltchik, Torsten Hoefler: “Slim Graph: Practical Lossy Graph Compression for Approximate Graph Processing, Storage, and Analytics”. Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (SC19), November 2019.