By Rob Farber on behalf of the Exascale Computing Project
First developed in 1998, the hypre team has adapted their cross-platform high performance library to support a variety of machine architectures over the years. Hypre supports scalable solvers and preconditioners that can be applied to large sparse linear systems on parallel computers.[i] Their latest work now gives scientists the ability to efficiently utilize modern GPU-based extreme scale parallel supercomputers to address many scientific problems.[ii]
As part of their Exascale Computing Project (ECP) funded effort, the hypre team has created a version of their algebraic multigrid (AMG) solver and preconditioner BoomerAMG [iii] that can capitalize on the SIMD (Single Instruction Multiple Data) computational model utilized by GPUs. Ulrike Meier Yang (leader of the Extreme-scale Scientific Software Development Kit for the ECP and the Mathematical Algorithms and Computing group at Lawrence Livermore National Laboratory (LLNL) notes, “Development of the GPU-friendly version required modularization of BoomerAMG into smaller kernels and some significant head-scratching and out-of-the-box thinking by the hypre team to create a new interpolation algorithm, which is an important AMG component. This SIMD-friendly interpolation method eliminates the need for a complex series of conditional operations that can slow GPU performance. Coupled with various additional code improvements by the hypre developers, the GPU version of the AMG algorithm can deliver better-than-CPU performance on suitable problems.“
Development of the GPU-friendly version required modularization of BoomerAMG into smaller kernels and some significant head-scratching and out-of-the-box thinking by the hypre team to create a new interpolation algorithm, which is an important AMG component. This SIMD-friendly interpolation method eliminates the need for a complex series of conditional operations that can slow GPU performance. Coupled with various additional code improvements by the hypre developers, the GPU version of the AMG algorithm can deliver better-than-CPU performance on suitable problems. – Ulrike Meier Yang, leader of the Extreme-scale Scientific Software Development Kit for the ECP and the Mathematical Algorithms and Computing group at LLNL
Yang’s caveat — “on suitable problems“– is an important, but not necessarily serious, limitation because the hypre library is used by research institutions and private companies to simulate a wide variety of physical systems including groundwater flow, magnetic fusion energy plasmas in tokamaks and stellarators, blood flow through the heart, fluid flow in steam generators for nuclear power plants, and pumping activity in oil reservoirs, to name just a few areas. In 2007, hypre won an R&D 100 award from R&D Magazine as one of the year’s most significant technological breakthroughs. [iv] Sometimes size limitations and other constraints imposed by the partial differential equations (PDEs) used to model the physical system unavoidably limit performance on SIMD computer architectures. In such cases, the cross-platform benefits provided by the hypre team become apparent, as scientists simply run on CPU-based systems.
For applicable problems, the following performance comparison on a representative coupled 3D Poisson benchmark with three variables shows that the AMG-preconditioned conjugate gradient method can indeed run faster on a GPU. Figure 1 below shows the Poisson benchmark can be solved faster on the GPU as indicated by the shorter runtime indicated on the y-axis. Figure 1 also shows that the GPU performance improvement increases as the size of the 3D grid increases. These results also show that the same runs between 1.6x and 3.2x faster on the GPU (the red line) compared to the same code running on 640 IBM Power 9 processor cores (the blue line). The SIMD-friendly method is also 2.1x to 3.8x faster than the previous hypre CPU implementation running on 640 IBM Power 9 processor cores (the green line).
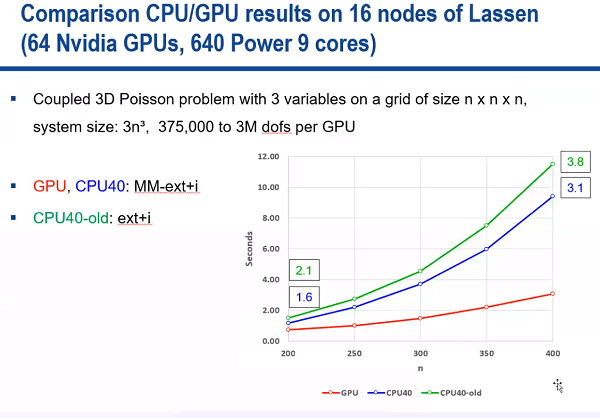
Figure 1: Performance increase observed when running the new GPU-accelerated method as compared to the same code running on 640 IBM Power 9 processor cores and the previous CPU-only hypre implementation also running on the IBM Power 9 processor cores.
Access to a performant GPU-based AMG library means that a large number of ECP projects will be able to efficiently utilize the GPU-accelerated architectures in the newest generation of exascale supercomputers. For example, 11 ECP software products, namely ExaConstit, XGC, chombo-crunch, libCEED, MARBL, PeleLM, TruchasPBF, Nalu-Wind, MFEM, ExaMPM, and Diablo, are listed as depending critically on hypre and the nine ECP software products, FLASH5, Castro, AMReX, PETSc/TAO, GEOSX, AMPE, Trilinos, xSDK, and SUNDIALS as having important dependencies on hypre. These products include application codes as well as popular scientific libraries that are heavily used in the HPC community outside of the ECP. Yang notes that currently the GPU version is CUDA-based. Work is in progress to convert the CUDA kernels to HIP for AMD GPUs and DPC++ for Intel GPUs.
The SIMD-friendly Idea
AMG methods basically have two phases as shown in Figure 2 below. The generation of the interpolation operator is a key part of the Setup Phase.

Figure 2: AMG methods have a Setup and Solve Phase
Some applications, e.g., applications that solve time dependent problems, need to set up AMG only once or every so often while performing the solve phase many times. In that case, larger GPU speedups can be achieved, as shown in Figure 3, which amends the benchmark results shown in Figure 1 with the GPU speedup for the Setup and Solve phases.
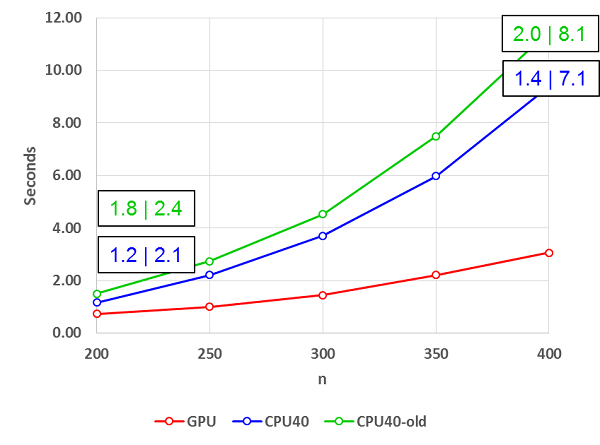
Figure 3: The Figure 1 results amended to include Setup|Solve runtime speedups
Basically, geometric multigrid methods start with a fine grid as shown in Figure 4 (below) but will move to coarser grids to efficiently damp out smooth errors that cannot quickly be resolved on finer grids. This leads to a fast-converging scalable method. Algebraic methods do not have grids, and are applied to a linear system, but use a similar concept to smooth out slow error components on increasingly smaller systems. Coarse grid matrices are generated by multiplying three sparse matrices as can be seen in Figure 2. This can lead to increasing communication demands on coarser grids and a large communication overhead which means the MPI communication time can limit performance. Another challenge is presented by the decreasing system sizes on coarser grids, since the per grid point computation gets too small which leads to computational inefficiencies that again limit performance.
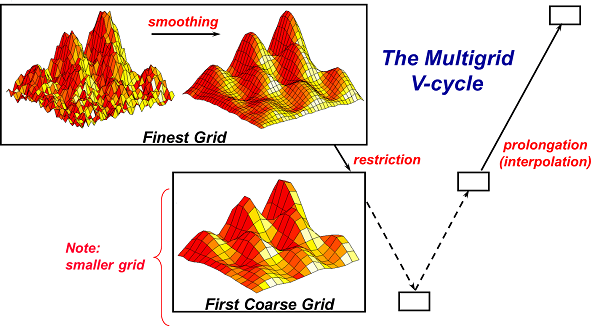
Figure 4: Multigrid uses coarse grids to efficiently damp out smooth error components
After evaluating AMG components for their potential for GPU-friendly implementation, the hypre team realized that conditional operations in the interpolation method would seriously limit performance. Nested conditional operations are known to cause severe performance degradation on SIMD architectures. [v]
The key insight was to create a new class of interpolation method that is efficient on SIMD architectures. These new methods can be formulated using matrix/vector and matrix/matrix operations that do not have nested conditional operations.[1] Ruipeng Li, computational mathematician and hypre developer at LLNL, comments: “Expressing AMG interpolation operators in terms of standard matrix operations has the following three advantages: First, it simplifies the implementation and increases portability to heterogeneous platforms. Second, it enhances the performance by utilizing available sparse kernels that can be potentially further optimized. Finally, of interest to mathematicians, it enables easier analysis of AMG approximation properties.” The benefit shown in Figure 3 demonstrates that
- overall time-to-solution is faster when using the new method on both CPUs and GPUs, and
- larger speedups for the GPU can be achieved in the solve phase.
Overall, the AMG solver utilizing the new method (and benefitting from other GPU optimizations) delivers a 3.1x to 3.8x faster time-to-solution. In particular, the solve phase runs between 7.1x and 8.1x faster as shown in Figure 3.
Summary
The new GPU-enabled hypre library opens the door to GPU acceleration for a number of ECP libraries and applications. With this library, scientists now have the ability to use GPUs and potentially realize significantly faster time-to-solution. This makes hypre a valuable addition to the HPC scientist’s toolset to run efficiently on a number of different machine architectures. Of course, any performance gain (or loss) is strongly affected by the characteristics of the PDEs being solved.
Users can download hypre from github. The hypre library is also included in the E4S software stack and can be used through PETSc and Trilinos.
Rob Farber is a global technology consultant and author focused on HPC and machine learning technology development that he applies at national labs and commercial organizations. He can be reached at info@techenablement.com.
[1] Ruipeng Li, Bjorn Sjogreen, Ulrike Meier Yang, “A New Class of AMG Interpolation Methods Based on Matrix-Matrix Multiplications”, to appear in SIAM Journal on Scientific Computing.
[i] Various special hypre solvers (e.g., Maxwell solver AMS, ADS, pAIR, MGR) built on BoomerAMG will benefit from this new strategy
[ii] https://computing.llnl.gov/projects/hypre-scalable-linear-solvers-multigrid-methods
[iii] https://www.sciencedirect.com/science/article/pii/S0168927401001155
[iv] https://computing.llnl.gov/projects/hypre-scalable-linear-solvers-multigrid-methods
[v] https://www.sciencedirect.com/book/9780123884268/cuda-application-design-and-development