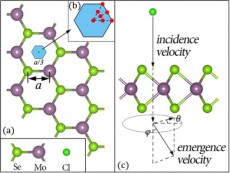
Model of ion (Cl) collision with atomically thin semiconductor (MoSe2). Collision region is shown in blue and zoomed in; red points show initial positions of Cl. The simulation calculates the energy loss of the ion based on the incident and emergent velocities of the Cl.
Researchers at LBNL have have developed a new algorithm that opens the door for real-time simulations in atomic-level materials research.
When electronic states in materials are excited during dynamic processes, interesting phenomena such as electrical charge transfer can take place on quadrillionth-of-a-second, or femtosecond, timescales. Numerical simulations in real time provide the best way to study these processes, but such simulations can be extremely expensive. For example, it can take a supercomputer several weeks to simulate a 10-femtosecond process.
One reason for the high cost is that real-time simulations of ultrafast phenomena require small time steps to describe the movement of an electron, which takes place on the attosecond timescale—a thousand times faster than the femtosecond timescale.
To combat the high cost associated with the small time steps, Lin-Wang Wang, senior staff scientist at Lawrence Berkeley National Laboratory (Berkeley Lab), and visiting scholar Zhi Wang from the Chinese Academy of Sciences, have developed a new real-time time-dependent density function theory (rt-TDDFT) algorithm that increases the small time step from about one attosecond to about half a femtosecond. This allows them to simulate ultrafast phenomena for systems of around 100 atoms, and opens the door for efficient real-time simulations of ultrafast processes and electron dynamics, such as excitation in photovoltaic materials and ultrafast demagnetization following an optical excitation.
We demonstrated a collision of an ion [Cl] with a 2D material [MoSe2] for 100 femtoseconds. We used supercomputing systems (NERSC’s Cray XE6 system, Hopper) for 10 hours to simulate the problem—a great increase in speed,” said L.W. Wang. That represents a reduction from 100,000 time steps down to only 500.
The results of the study were reported February 15, 2015, in Physical Review Letters.
Reducing the Dimension of the Problem
Conventional computational methods cannot be used to study systems in which electrons have been excited from the ground state, as is the case for ultrafast processes involving charge transfer. But using real-time simulations, an excited system can be modeled with time-dependent quantum mechanical equations that describe the movement of electrons.
The traditional algorithms work by directly manipulating these equations. Wang’s new approach, which involves adding a new algorithm on top of his PEtot (parallel total energy) code, originally developed by Wang when he worked at the National Renewable Energy Laboratory and later parallelized by Wang and Andrew Canning after Wang moved to NERSC in 1999. PEtot is a plane-wave pseudopotential density functional ground-state calculation package designed for large system simulations to be run on large parallel computers and Linux cluster machines.
With this new algorithm, the rt-TDDFT simulation can have comparable speed to the Born-Oppenheim ab initio molecular dynamics simulations,” the researchers wrote in the Physical Review Letters paper.
To achieve this, the algorithm expands the equations in PEtot into individual terms, based on which states are excited at a given time. The challenge, which Wang has solved, is to figure out the time evolution of the individual terms. The advantage is that some terms in the expanded equations can be eliminated.
By eliminating higher energy terms, you significantly reduce the dimension of your problem, and you can also use a bigger time step,” explained Wang, describing the key to the algorithm’s success: Solving the equations in bigger time steps reduces the computational cost and increases the speed of the simulations.
Comparing the new algorithm with the old, slower algorithm yields similar results, e.g., the predicted energies and velocities of an atom passing through a layer of material are the same for both models, he noted.
Being able to run the code on a supercomputer like Hopper for long periods of time was central to the success of this study, according to Wang.
The new supercomputers are critical, and so are the fast processors,” he said. “This code does not necessarily scale to many processors. Typically we use a few hundred processors. But the long time run is critical.”
Source: Lawrence Berkeley National Laboratory.



